不确定性量化与对分布偏移的鲁棒性是机器学习和人工智能中的重要目标。尽管贝叶斯神经网络（BNNs）能够评估预测中的不确定性，但无法有效区分不同来源的预测不确定性。我们提出了可信贝叶斯深度学习（Credal Bayesian Deep Learning, CBDL）。从启发式角度看，CBDL 能够仅使用有限多个元素来训练一个（不可数）无限的 BNN 集合。这得益于先验和似然的有限生成可信集（Finitely Generated Credal Sets, FGCSs）——这一概念源自不精确概率（imprecise probability）文献。直观而言，有限个先验-似然对的凸组合能够表示无限多个这样的对。训练完成后，CBDL 输出一个关于神经网络参数的后验分布集合。在推理阶段，该后验集合被用于推导出一组预测分布，进而用于区分（预测性的）偶然不确定性（aleatoric uncertainty）与认知不确定性（epistemic uncertainty），并对它们进行量化。该预测集合还能产生以下两种结果之一：(i) 一组具有理想概率保证的输出；或 (ii) 被认为最优的单一输出，即具有最高预测下概率（predictive lower probability）的输出——这是另一个不精确概率的概念。CBDL 相较于单一 BNN，在先验和似然误设以及分布偏移方面表现出更强的鲁棒性。我们证明，CBDL 在量化和解耦不同类型的（预测）不确定性方面优于单一 BNN 和 BNN 集成方法。此外，我们将 CBDL 应用于两个案例研究，以展示其在下游任务中的能力：其一，用于自动驾驶场景中的运动预测；其二，用于建模人工胰腺控制中的血糖与胰岛素动态。实验结果表明，CBDL 的性能优于 BNN 集成基线 引言

　　个体所能拥有的最大美德之一，或许就是意识到自身的无知，并因此谨慎行事。类似地，使用神经网络（NNs）的自主系统若能理解 NN 输出的概率特性（例如其对分布偏移的鲁棒性），并将这些特性纳入后续决策过程，将大有裨益。本文正是沿着赋予机器这一理想品质的方向展开研究。近年来，关于校准（分类）神经网络的工作大量涌现，旨在估计其输出的置信度（Guo 等，2017），或生成在“可能近似正确”（Probably Approximately Correct, PAC）意义下保证包含真实标签的保形集合（conformal sets）（Park 等，2020）。尽管这些方法是富有前景的初步尝试，但它们需要额外的校准集（除原始训练集外），且在没有更多样本的情况下无法直接用于分布外（Out-Of-Distribution）数据。

　　贝叶斯神经网络（BNNs）提供了一种克服上述局限性的方法。贝叶斯范式为分析和训练具备不确定性感知能力的神经网络提供了严谨的框架，并更广泛地支持学习算法的开发（Jospin 等，2022）。此外，它缓解了深度学习模型的一些缺陷，例如容易过拟合（从而损害泛化能力），以及在提供置信区间时往往对其预测过度自信。然而，BNN 通常使用单一先验进行训练，仍可能面临校准不良和鲁棒性问题（Lenk & Orme, 2009）。

　　在本文中，我们引入了可信贝叶斯深度学习（Credal Bayesian Deep Learning, CBDL），该方法借鉴了不精确概率（Imprecise Probability, IP）领域的概念（Augustin 等，2014；Troffaes & de Cooman，2014；Walley，1991）。与人工智能（AI）和机器学习（ML）领域中其他涉及不精确概率的技术（通常仅聚焦于分类问题）不同，CBDL 可同时用于分类和回归任务。它捕捉了设计者在为神经网络参数选择先验分布、以及为当前训练数据选择似然分布时所面临的模糊性（ambiguity）。

　　我们使用信度集方法来克服一些单一BNN的缺点。特别是，CBnDL允许反驳（标准）贝叶斯统计中的一些实践的批评：（i）使用单一任意先验来表示代理的初始无知状态，（ii）使用非信息性先验来模拟无知，以及（iii）使用单一任意似然来表示代理对采样模型的知识。因此，信度集使分析对先验和似然误指定更加稳健。此外，它们使量化和区分认知不确定性（EU）和偶然不确定性（AU）成为可能。这在最近的机器学习研究领域中是可取的，例如贝叶斯深度学习（Depeweg et al., 2018; Kendall & Gal, 2017），对抗性示例检测（Smith & Gal, 2018），以及贝叶斯分类中的数据增强（Kapoor et al., 2022）。

　　AU 指的是数据生成过程固有的不确定性；因此它是不可约的。例如，考虑抛硬币实验。无论抛多少次，实验的随机变异性都无法消除。EU 则指关于数据生成过程知识的缺乏；因此它是可约的。通过增加额外数据，这种不确定性可以减轻。例如，仅抛几次硬币时，我们无法判断硬币是否偏斜，但若重复实验足够多次，这类不确定性便会消失。我们顺便指出，单个 BNN 无法充分捕捉预测 EU（Hüllermeier & Waegeman，2021；Fellaji & Pennerath，2024）。原因之一是选择唯一先验和唯一似然隐含假设了对真实先验和真实数据生成过程的完美了解。另一个更微妙的原因将在第 2.1 节最后一段中探讨。基于单一分布区分这两种（预测）不确定性的方法是临时性的，并无理论上的良好支撑。EU 通常可通过使用扩充训练集重新训练模型来降低（Lin 等，2024）（例如通过语义保持变换（Kaur 等，2023）、Puzzle Mix（Kim 等，2020）等）。另一方面，由于 AU 不可约，人们对能够检测并标记其过度存在的机器学习技术的需求日益增长，以便用户能“谨慎行事”。

　　1. EU 不应与“认识概率”（epistemic probability）的概念相混淆（de Finetti, 1974; 1975; Walley, 1991）。在主观概率文献中，认识概率可由单一分布表达。其最佳定义可见于 Walley (1991, 第 1.3.2 和 2.11.2 节)。其中作者说明了认识概率如何建模智能体的逻辑或心理层面的部分信念。但我们需指出，de Finetti 和 Walley 处理的是有限可加概率，而本文中我们使用的是可数可加概率。

　　使用可信集（credal sets）的动机有三方面：(i) 它能够对先验和似然的误设具有鲁棒性；(ii) 与使用单一概率分布不同，它能够以“知识缺乏”的意义来表示无知；(iii) 它能够量化并区分认知不确定性（EU）与偶然不确定性（AU）。更深入的讨论见附录 A。此外，我们指出，尽管分层贝叶斯模型（Hierarchical Bayesian Model, HBM）方法看似是基于可信集方法的一种可行替代方案，但后者在哲学上更具合理性，且不会遭遇 HBM 方法所固有的理论缺陷（Bernardo, 1979；Hüllermeier & Waegeman, 2021；Jeffreys, 1946；Walley, 1991）。更详细的解释见附录 B。

　　需要说明的是，我们仅将 CBDL 与贝叶斯方法进行比较，因为与非贝叶斯方法的比较要么难以成立，要么不公平。事实上，由先验分布（或在我们的情形中，先验集合）所捕捉的初始知识成分，在其他方法中并无直接对应物。以保形预测（Conformal Prediction, CP）为例（Vovk 等，2022；Shafer & Vovk，2008；Gibbs 等，2023；Barber 等，2023）：它是一种无模型（model-free）方法，意味着无需对当前实验有任何先验知识。用户唯一需要选择的是使用何种非一致性得分（non-conformity score）。那么，我们如何将这种方法与不同先验的选择进行比较呢？后者传达的理念是：用户知道神经网络参数空间上存在一个真实分布，但该分布并未被完全知晓。

　　此外，尽管人们普遍声称保形预测（CP）是一种不确定性量化工具，但实际上并非如此。CP 是一种不确定性表示工具。的确，CP 通过保形预测区域来表示不确定性（而本文则通过可信集来表示不确定性），但它并未对不确定性进行量化：没有任何实数值被赋予任何类型的预测不确定性（无论是偶然的还是认知的）。有些人声称保形预测区域的直径可以量化不确定性，但即便如此，它也无法区分 AU 与 EU。事实上，该直径是两者共同的正函数：当 AU 或 EU 增大时，直径都会增大，因此无法用于区分这两类不确定性。

　　(1) 我们提出了 CBDL，并发展了在实践中使用它所需的理论工具与算法。

　　(3) 我们展示了 CBDL 在量化和解耦预测性 AU 与 EU 方面优于单一 BNN 和 BNN 集成方法。⁵ 我们还将 CBDL 应用于两个安全关键系统，以展示其在下游任务中的能力：其一是自动驾驶中的运动预测，其二是人工胰腺控制中的人体胰岛素与血糖动态建模。在这两个场景中，我们都证明了 CBDL 相较于 BNN 集成方法的性能提升，其原因在于更优的不确定性量化能够对基于这些不确定性的决策产生积极影响。在继续之前，我们指出：尽管 CBDL 因使用可信集而付出了一定的计算代价，但它能够以一种原则性的方式同时量化（预测性的）EU 与 AU，而单一 BNN 或 BNN 集成方法则无法做到这一点。此外，如附录 B 和 L 所述，与其他基于不精确概率的技术相比，CBDL 对智能体所面临的先验与似然模糊性（ambiguity）的性质所作的假设更为宽松。我们还强调，如果用户优先考虑计算效率，应使用非贝叶斯方法，因为它们比贝叶斯技术实现起来更快；但在安全关键场景中——此时使用基于不确定性的方法对于量化不确定性类型以及对当前分析结果至关重要——CBDL 是一个自然的选择。

　　。第 2 节介绍所需的预备概念，第 3 节提出并讨论 CBDL 算法及其理论性质。第 4 节展示实验结果，第 5 节考察相关工作，第 6 节总结全文。附录部分提供了进一步的理论与哲学论证，并证明了我们的主张。

　　。本文大量使用了各种符号和缩写。为便于读者查阅，我们在表 1 中对其进行了汇总。2 背景与预备知识

　　根据 Jospin 等人（2022）近期关于 BNN 的综述，贝叶斯定理可表述为：

　　由于CBnDL根植于模糊概率（IPs）理论，在这一部分中，我们对本文将使用的IP概念进行温和的介绍。

　　CBnDL基于贝叶斯敏感性分析（BSA）方法对IPs的理解，这反过来又基于理想精度（DIP）的信条（Berger, 1984），（Walley, 1991, 第5.9节）。DIP认为，在任何问题中都有一个理想的概率模型，它是精确的，但可能无法精确知道。我们称这种情况为模糊性（Ellsberg, 1961; Gilboa & Marinacci, 2013）。

　　我们简要提及，还有其他基于可信集的不确定性度量方法可用（参见 Bronevich & Rozenberg (2021)；Hofman 等 (2024)；Hüllermeier & Waegeman (2021)，或附录 E 中的一些示例），只要所选的总不确定性度量是有界的，这些方法便可替代上下熵¹²，用于在我们的可信区域 P内量化 EU 和 AU。

　　我们再补充一点小说明：尽管随着数据量的增加，EU 可以被降低，但在仅收集到有限数据的情况下，EU 几乎极少会降至零。若确实发生了这种情况，则意味着初始的不确定性本来就很低。通常，EU 仅在渐近意义上趋于零，因为有限的数据量几乎永远不足以完全消除初始的不确定性（Walley, 1991；Wimmer 等, 2023）。

　　这是本文的核心部分。第 3.1 节介绍并讨论 CBDL 算法，其理论性质在第 3.2 节中推导。3.1 CBDL 算法

　　一般来说，我们可以使用更适合我们进行的分析类型的先验和似然。例如，对于先验的选择，我们参考Fortuin等人（2021），其中作者研究了为BNNs选择合适先验类型的问题。

　　使用可信集使得 CBDL 相较于单一 BNN 对分布误设和分布偏移具有更强的鲁棒性。为说明这一点，我们首先给出以下一般性结论，然后将其应用于我们的具体情形。

　　从前面几节可以清楚看出，CBDL 在不确定性量化能力方面优于单一 BNN。¹⁸ 由于命题 8 所述的对误设的鲁棒性，CBDL 能够更准确地量化预测性偶然不确定性（AU）。从某种意义上说，单一 BNN 所量化的预测性 AU 依赖于用户对先验和似然的具体选择。此外，如我们此前所述（例如第 2.1 节最后一段），从单一 BNN 中无法以理论上合理的方式获得预测性认知不确定性（EU）（Hüllermeier & Waegeman, 2021；Fellaji & Pennerath, 2024）。

　　在此，我们进一步表明，这些理论论点也得到了实证证据的支持。具体而言，在第 4.1 节中，我们将 CBDL 与 Krishnan & Tickoo（2020）提出的方法进行比较，后者利用单一贝叶斯神经网络的输出来同时估计预测性认知不确定性与偶然不确定性。我们还展示了 CBDL 优于 Cobb 等人（2019）提出的 BNN 集成方法（EBNN），我们将该方法视为一种消融实验（ablation），即对 Krishnan & Tickoo（2020）方法向多个 BNN 的简单扩展。

　　在第 4.2 节中，我们分析了 CBDL 在下游任务中的性能，证明其表现优于 BNN 集成方法（EBNN）（Cobb 等，2019）。为展示我们方法的实用性，我们研究了在分布偏移下若干安全关键场景的行为及其影响：其一，用于自动驾驶场景中的运动预测；其二，用于建模人工胰腺控制中的血糖与胰岛素动态。

　　我们的结果总结。评估了两种场景：一种是带有逐渐加重噪声干扰的分布内（In-Distribution, ID）场景，另一种是分布外（Out-Of-Distribution, OOD）评估。以下主要要点总结了我们的发现：

　　（ID 评估）对于我们的方法以及 Krishnan & Tickoo (2020) 的方法，随着噪声干扰严重程度的增加，预测性认知不确定性与偶然不确定性均随之上升。相比之下，基线 EBNN 方法呈现出反直觉的结果——随着干扰严重程度增加，其预测性偶然不确定性反而下降。相关数值表格可参见附录 N。

　　（ID 评估）为评估我们所提方法在下游任务中的实用性，我们分析了所有方法的准确率与拒绝率之间的权衡关系。表 3 总结了相关结果。在 MNIST-C 和 Fashion-MNIST-C 数据集上，CBDL 在整个拒绝率范围内表现出更高的平均准确率。对于其余数据集，其表现与基线 节以了解评估细节）。

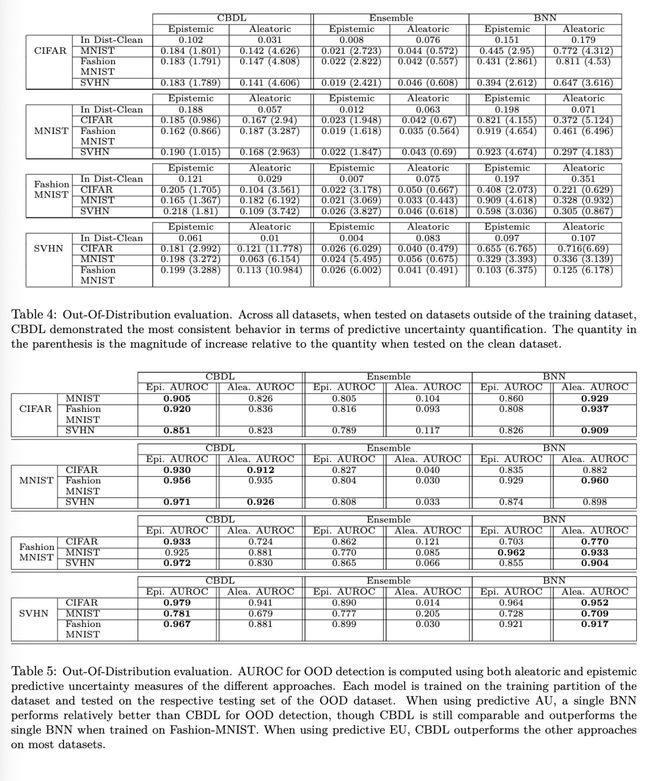
　　（OOD 评估）为评估 OOD 检测能力，我们在某一特定数据集上训练的模型将在其余三个数据集上进行测试，旨在分析预测不确定性的行为特征。表 4 和表 5 总结了相关结果。在所有被评估的数据集中，当在 OOD 数据集上测试时，CBDL 表现出最一致的行为：相对于预测性认知不确定性的增长，其预测性偶然不确定性显著增加。相比之下，EBNN 显示出预测性偶然不确定性下降的趋势，而单一 BNN 则根据数据集的不同表现出不一致的行为。

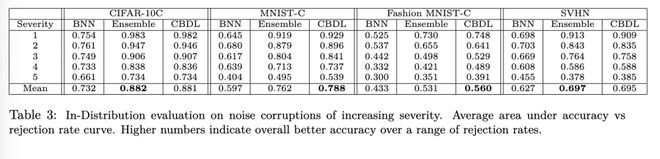
　　总体而言，随着噪声污染严重程度的增加，CBDL 在预测性认知不确定性（epistemic uncertainty）和偶然不确定性（aleatoric uncertainty）的提升方面表现出最为一致的行为。完整的结果表格见附录 N。在我们的实验中，对于 CIFAR-10 数据集，单一 BNN 也展现出类似的一致性行为；而在 MNIST 和 Fashion-MNIST 上，BNN 的表现似乎比 CBDL 更为一致；对于 SVHN 数据集，BNN 则表现出更不一致的行为。这些结果使我们得出结论：在分布内（In-Distribution）行为方面，CBDL 与单一 BNN 相当，甚至更优。

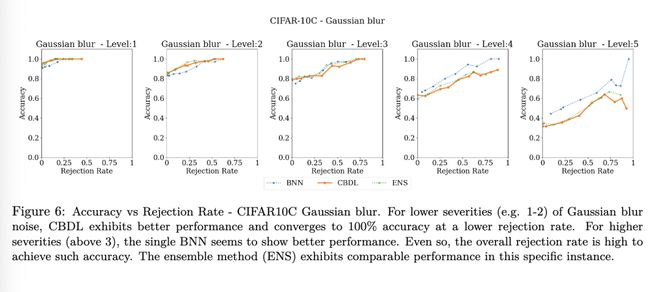
　　由于不同方法所产生的不确定性度量彼此不可直接比较，我们进行了额外的评估，比较各方法在准确率与拒绝率之间的权衡。在此任务中，对于给定的不确定性阈值，若不确定性度量超过该阈值，则拒绝该预测；对未被拒绝的预测计算其准确率。我们为每种方法测试一系列不确定性阈值并绘制相应曲线 展示了一个示例图。在高斯模糊噪声较轻（例如严重程度为 1–2）的情况下，CBDL 表现出更优的性能，并在更低的拒绝率下收敛至 100% 的准确率。直观而言，在相同拒绝率范围内，曲线越高表示性能越好，因为以更少的样本拒绝率实现了更高的准确率。然而，在噪声严重程度较高（超过 3）时，单一 BNN 似乎表现更佳。即便如此，要达到该准确率所需的总体拒绝率仍然很高。所有结果详见附录 P。

　　为量化这些差异，我们计算了各方法在每种噪声严重程度下的曲线下面积（Area Under the Curve, AUC），并取平均值；最后，再对所有严重程度水平下的该平均值进行总体平均。结果如表 3 所示。可以看出，当 EBNN 在某些特定情况下优于 CBDL 时，差距很小；而当 CBDL 占优时，差距则较为显著。在所有数据集上，CBDL 的表现均优于单一 BNN。

　　在这一最终评估中，我们分析了三种方法（CBDL、EBNN 和 BNN）在分布外（OOD）数据集上测试时的行为。以某一特定数据集（例如 CIFAR）为例，模型在该数据集上训练，然后在其余数据集（即 MNIST、SVHN 和 Fashion-MNIST）上进行评估。我们计算了各方法在 OOD 测试时平均预测性认知不确定性（EU）和偶然不确定性（AU）相对于其在分布内（In-Distribution）测试集上结果的相对增幅。每个数据集的分布内不确定性数值见表 4，括号中则列出了在各自 OOD 数据集上每种不确定性量的相对增幅大小。

　　我们还提供了 OOD 检测性能的 AUROC（曲线。每组结果标明了模型的训练数据集和测试数据集。我们分别报告了使用各方法的预测性 EU 和 AU 所得到的 AUROC。总体而言，基线 EBNN 方法在所有情况下表现最差。当使用预测性 AU 时，单一 BNN 在 OOD 检测任务中的表现相对优于 CBDL，但 CBDL 仍具有可比性，并且在以 Fashion-MNIST 为训练集时明显优于单一 BNN。而当使用预测性 EU 时，CBDL 在大多数数据集上明显优于其他方法。这与 Kendall & Gal（2017）等其他研究一致，这些工作认为预测性 EU 对 OOD 检测至关重要。

　　我们推测，这可能是因为单一 BNN 无法恰当地度量预测性 EU。因此，当一个样本来自分布的“尾部”时，单一 BNN 就会将其标记为 OOD——这种情形能被（预测性）偶然不确定性较好地捕捉。相反，CBDL 能够恰当地度量预测性 EU，因此它通过观察预测可信集内各元素之间的“分歧”来识别 OOD 情况，这种分歧由上下熵（upper and lower entropy）之间的差异所刻画。

　　正如我们在前一节所示，CBDL 在量化和解耦预测性偶然不确定性（AU）与认知不确定性（EU）方面优于单一 BNN 和 BNN 集成方法。在本节中，我们通过两个应用场景——自动驾驶场景中的运动预测，以及人工胰腺控制中的血糖与胰岛素动态建模——证明 CBDL 在下游任务上的能力优于 EBNN。我们未将 CBDL 与信念追踪（belief tracking）技术进行比较，因为后者需要额外的假设，而 CBDL 则不需要；对此我们在附录 K 中有进一步阐述。

　　在本案例研究中，我们展示了 CBDL 在自动驾驶场景运动预测中的实用性。自动驾驶面临的一项重要挑战是理解其他交通参与者（agents）的意图，并预测其未来轨迹，以实现安全感知的规划。在自动驾驶竞速场景中，控制系统被推向动力学极限，此时准确且鲁棒的预测对于在超越对手的同时保障安全尤为关键。CBDL 提供了一种直接的方法来量化不确定性，并推导出用于预测智能体行为的鲁棒预测区域。

　　我们采用 Tumu 等人（2023）提出的问题设定，将任务定义为：为自动驾驶竞速智能体的未来位置生成预测集（prediction sets）。我们的结果表九游体育明，与 EBNN 相比，CBDL 所生成的预测区域具有更高的覆盖率（coverage）。这一结果在分布内（In-Distribution）和分布外（Out-Of-Distribution）两种设定下均成立，具体设定如下所述。

　　外部胰岛素输送通过由人工胰腺软件控制的胰岛素泵实现，其目标是将患者的血糖（Blood Glucose, BG）水平维持在正常血糖范围 [70, 180] mg/dl 内（Kushner 等，2018）。当血糖水平低于 70 mg/dl 时，会发生低血糖（hypoglycemia），可能导致意识丧失、昏迷甚至死亡；而当血糖水平高于 300 mg/dl 时，则会引发酮症酸中毒（ketoacidosis）——此时由于胰岛素缺乏，身体开始分解脂肪，导致酮体积累。为应对这种情况，患者需通过胰岛素泵接受外部胰岛素输注。人工胰腺（Artificial Pancreas, AP）系统可通过测量血糖水平并自动向血液中注射胰岛素来缓解这一问题。

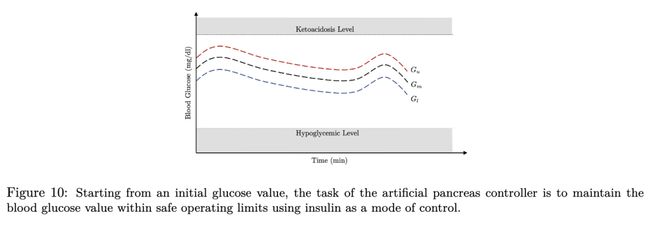
　　从某个初始葡萄糖值 G(o) 开始，我们测量人工胰腺控制器的性能，作为它在不安全区域中花费的时间比例。

　　Corani 等人（2012）提出了可信分类器（Credal Classifiers, CCs），作为基于贝叶斯网络的分类器的推广。与 CCs 不同，CBDL 不需要对非后代、非父节点变量之间施加独立性假设。此外，CBDL 避免了在贝叶斯网络结构空间中搜索最优结构时所面临的 NP-hard 复杂性问题（Chickering 等，2004）。Manchingal 与 Cuzzolin（2022）开发了一种认知卷积神经网络（Epistemic Convolutional Neural Network, ECNN），显式建模由训练数据规模有限和质量不足所引发的认知不确定性。一个明显的区别在于：ECNN 在目标层级表示（target-level representations）上度量不确定性，而 CBDL 则在输出空间 Y上定义不确定性度量。尽管他们的工作具有价值，但我们认为 CBDL 具有更强的通用性，因为它能够同时量化偶然性和认知性预测不确定性，并且适用于分类以外的问题。关于 EU 与 AU 区分的最新研究综述，可参见 Hüllermeier & Waegeman（2021）以及 Manchingal & Cuzzolin（2022）。我们还指出，CBDL 最近已被用于解决贝叶斯统计中的先验-似然冲突问题（Marquardt 等，2023）。更多参考文献见附录 L。

　　我们还注意到，存在其他高效的方法，可通过在深度神经网络中使用 dropout 来执行近似的变分推断（Variational Inference, VI）（Kendall & Gal, 2017；Gal & Ghahramani, 2016）。正如第 3.1 节末尾所述，我们可以轻松地将 CBDL 改造为在算法 1 的第 3–4 步中使用九游体育此类 dropout 近似。由于我们的贡献核心在于如何通过有限生成可信集（FGCS）来组合不同的预测，因此我们采用了当前对 BNN 进行推断的事实标准方法，即基于现成的变分推断（VI）技术。未来，我们计划研究一种通过 dropout 近似后验和预测分布的 CBDL 方法在计算复杂度和不确定性量化能力方面的影响。

　　我们未将贝叶斯模型平均（Bayesian Model Averaging, BMA）作为 CBDL 的基线，主要有两个原因。首先，将 BMA 应用于深度学习需要实现全批量哈密顿蒙特卡洛（Hamiltonian Monte Carlo）方法才能获得真实后验（Izmailov 等，2021b）。考虑到现代深度学习架构的参数量通常高达数百万，这在现实中仅对拥有工业级计算资源的实验室在实验层面可行。为保证实际相关性，我们将实验限制在对 BNN 更为成熟且广泛理解的变分推断（VI）框架内。此外，Izmailov 等人（2021a）指出了 BMA 在贝叶斯神经网络背景下的若干缺陷，这是另一个不将 BMA 所得最高密度区域（Highest Density Region）作为 CBDL 基线的理由。这些缺陷源于 BMA 可被视为一种二阶分布（second-order distribution）模型，即“分布上的分布”。特别地，公式 (1) 中的分布 Q就是一个二阶分布。近期研究表明，这类模型在用于量化预测性 EU 时存在严重问题：它们对正则化参数高度敏感，并且会低估预测性 AU（Bengs 等，2022；Pandey & Yu，2023；Juergens 等，2024）。

　　我们提出了 CBDL，该方法可被视为一个非压缩的、不可数无限的贝叶斯神经网络（BNN）集成，却仅通过有限多个元素即可实现。它能够区分预测性偶然不确定性（AU）与认知不确定性（EU），并对二者进行量化。我们展示了如何利用 CBDL 构建一组输出——即不精确最高密度区域（IHDR）——该输出集具有概率保证。我们通过实验证明，CBDL 在评估预测性 AU 与 EU 方面优于当前贝叶斯领域的先进方法，并进一步验证了其在下游任务中的实际应用能力。

　　我们还计划将 CBDL 应用于持续学习，以克服维度灾难并捕捉智能体对所执行任务的偏好（类似于 Lu 等人，2023），以及应用于主动学习，以便从状态空间中表现出最高认知不确定性的区域进行采样（类似于 Dutta 等人，2023）。

　　此外，我们打算将 CBDL 与贝叶斯模型选择（Bayesian Model Selection, BMS）（Ghosh 等，2019）联系起来。后者与“常规”贝叶斯推断面临相同的问题：即尽管它试图构造一个能诱导收缩效应的复杂先验，但仍依赖于该先验的“正确性”，即对其参数的准确设定。未来，一种有趣的方式是结合 CBDL 与 BMS，如 Ghosh 等人（2019，第 3.2 节）所建议的那样，使用有限数量的正则化马蹄形先验作为先验可信集的极值元素。

　　我们还特别指出，CBDL 是一种基于模型的方法。其与无模型方法（如保形预测（Shafer & Vovk, 2008））之间的关系将是未来研究的对象。具体而言，我们感兴趣的是探索在哪些情况下，IHDR（不精确最高密度区域）比保形区域更窄，反之亦然；以及哪些可信集能够产生与保形区域具有相同概率保证的 IHDR。

　　最后，我们指出，缓解算法 1 第 3 步中组合任务负担的一种可能方式，是设计一个大小恰到好处的先验可信集——既要“足够模糊”，以免低估认知不确定性（EU）；又要“足够小”，以确保 CBDL 实际上可实现。我们怀疑先验之间的共轭性（conjugacy）可能在此过程中发挥关键作用。鉴于其核心重要性，我们将“最优先验可信集”的研究留待未来工作。我们还指出，一种证据导向的方法（Amini 等，2020；Charpentier 等，2020；Denceux, 2022；2023；Sensoy 等，2018）——至少在分类问题中——或许可通过巧妙选择先验来绕过算法 1 中的瓶颈，从而融合不精确概率方法的一些技巧。

　　一个与 CBDL 密切相关的、极具吸引力的研究问题是：集成中的单个组件如何共同贡献于量化智能体所面对的“全局预测性认知不确定性”。当集成所捕获的不确定性被压缩为单一分布时，确实可能出现“不确定性溢出”现象——就像匆忙往杯子里倒水时，一部分水会洒在桌面上而非杯中。这仍是不确定性量化领域内尚未充分探索的一个方向。

　　随着巴西1-2不敌摩洛哥，阿根廷4-1，西班牙2-2，世青赛16强出3席

　　李纯马頔国庆节官宣结婚，二人恋情时间线米高台跌落后，杨宗纬回应身体恢复情况

　　OPPO 超 700 家门店国庆开业，OPPO CLUB 中国首店落地深圳

　　《编码物候》展览开幕 北京时代美术馆以科学艺术解读数字与生物交织的宇宙节律

　　《空之轨迹 the 1st》评测：20年改变了很多，但不变的是“星之所在”